11TH Grade Science [Chemistry] |
|
|--SI units
|--Significant digits
|--History of Atomic Structure
|--Nucleus and electrons
|--Introduction to Quantum Theory
|--The Periodic Table
|--Ionic Bonds
|--Covalent Bonds
|--Molecular Shape
|--Chemical Equations
|--Balancing Equations
|--Types of Chemical Reactions
|--Energy changes in chemical reactions
|--Systems, States, and Thermodynamic Processes
|--The Three Laws of Thermodynamics
|--Chemical Thermodynamics
Required Textbook: A Beka, Precision & Design, Work-Text, Pensacola, Florida, current edition.
[a] Properties of Matter
[i] Differentiate between pure substances and mixtures based on physical properties such as density, melting point, boiling point, and solubility.
[ii] Determine the properties and quantities of matter such as mass, volume, temperature, density, melting point, boiling point, conductivity, solubility, color, numbers of moles, and pH (calculate pH from the hydrogen-ion concentration), and designate these properties as either extensive or intensive.
[iii] Recognize indicators of chemical changes such as temperature change, the production of a gas, the production of a precipitate, or a color change.
[iv] Describe solutions in terms of their degree of saturation.
[v] Describe solutions in appropriate concentration units (be able to calculate these units), such as molarity, percent by mass or volume, parts per million (ppm), or parts per billion (ppb).
[vi] Predict formulas of stable ionic compounds based on charge balance of stable ions.
[vii] Use appropriate nomenclature when naming compounds.
[viii] Use formulas and laboratory investigations to classify substances as metal or nonmetal, ionic or molecular, acid or base, and organic or inorganic.
[b] The Nature of Chemical Change
[i] Describe chemical reactions with balanced chemical equations.
[ii] Recognize and classify reactions of various types such as oxidation-reduction.
[iii] Predict products of simple reaction types including acid/base, electron transfer, and precipitation.
[iv] Use the principle of conservation of mass to make calculations related to chemical reactions. Calculate the masses of reactants and products in a chemical reaction from the mass of one of the reactants or products and the relevant atomic masses.
[v] Use Avogadro’s law to make mass-volume calculations for simple chemical reactions. Given a chemical equation, calculate the mass, gas volume, and/or number of moles needed to produce a given gas volume, mass, and/or number of moles of product.
[vi] Calculate the percent composition by mass of a compound or mixture when given the formula.
[vii] Perform calculations that demonstrate an understanding of the relationship between molarity, volume, and number of moles of a solute in a solution.
[viii] Use titration data to calculate the concentration of an unknown solution.
[ix] Predict how a reaction rate will be quantitatively affected by changes of concentration temperature, surface area, and the use of catalysts.
[x] Use oxidation states to recognize electron transfer reactions and identify the substance(s) losing and gaining electrons in an electron transfer reaction.
[c] The Structure of Matter
[i] Describe physical changes and properties of matter through sketches and descriptions of the involved materials.
[ii] Describe chemical changes and reactions using sketches and descriptions of the reactants and products.
[iii] Explain that chemical bonds between atoms in molecules, such as H2, CH4, NH3, C2H4, N2, Cl2, and many large biological molecules are covalent.
[iv] Perform calculations that demonstrate an understanding of the gas laws. Apply the gas laws to relations between pressure, temperature, and volume of any amount of an ideal gas or any mixture of ideal gases.
[v] Use kinetic molecular theory to explain changes in gas volumes, pressure, and temperature (Solve problems using pV=nRT).
[vi] Use an element’s location in the Periodic Table to determine its number of valence electrons, and predict what stable ion or ions an element is likely to form in reacting with other specified elements.
[vii] Use the Periodic Table to compare attractions that atoms have for their electrons and explain periodic properties, such as atomic size, based on these attractions.
[viii] Infer and explain physical properties of substances, such as melting points, boiling points, and solubility, based on the strength of molecular attractions.
[ix] Describe the nature of ionic, covalent, and hydrogen bonds and give examples of how they contribute to the formation of various types of compounds.
[x] Describe that spectral lines are the result of transitions of electrons between energy levels and that these lines correspond to photons with a frequency related to the energy spacing between levels by using Planck’s relationship (E=hν).
[d] The Nature of Energy and Change
[i] Distinguish between the concepts of temperature and heat.
[ii] Solve problems involving heat flow and temperature changes, using known values of specific heat and latent heat of phase change.
[iii] Classify chemical reactions and/or phase changes as exothermic or endothermic.
[iv] Describe the role of light, heat, and electrical energies in physical, chemical, and nuclear changes.
[v] Describe that the energy release per gram of material is much larger in nuclear fusion or fission reactions than in chemical reactions. The change in mass (calculated by E=mc2) is small but significant in nuclear reactions.
[vi] Calculate the amount of radioactive substance remaining after an integral number of half-lives have passed.
[e] The Basic Structures and Reactions of Organic Chemicals
[i] Convert between formulas and names of common organic compounds.
[ii] Recognize common functional groups and polymers when given chemical formulas and names.
0.1 - SI units
In chemistry, the characterization protocol of a substance often requires physical measurements. These measurements are reported in either base or derived SI units. There are seven base units; they are called base units because none of them can be expressed as combinations of the other six.
| QUANTITY | Length | Mass | Time | Temperature | Amount of Substance | Electric Current | Luminous Intensity |
| NAME/DEFINITION | Meter | Kilogram | Second | Degree (kelvin or Celcius) | mole | ampere | candela |
| SI UNIT | m | kg | s | K or 0C | mo | A | cd |
Other units can be built from the seven base units. Some widely used combinations of the base units are given special names to make working with them easier.
| QUANTITY | Area | Volume | Density | Speed | Acceleration | Force | Pressure | Energy |
| NAME/DEFINITION | Meter Squared | Meter Cubed | Mass per Unit Volume | Distance traveled per unit time | Speed change per unit time | Mass times acceleration | Force per unit Area | Force times Distance |
| SI UNIT | m2 | m3 | kg/m3 | m/s | m/s2 | kg/(m/s2) | kg/(m2/s2) |
Note that in order for the SI units to follow a certain pattern, the kilogram and the cubic meter are the SI units of mass and volume respectively. However, these quantities are impractical for use in chemistry. Instead, the gram and the liter are most widely used. One gram is equal to 1 X 10-3 kg and one liter is equal to 1 X 10-3 cubic meters. These quantities have been written with powers of ten. This is very commom in chemistry because the values to be reported are often larger or smaller than the base SI units. Such quantities are written with prefixes that represent multiples of ten.
| Prefix | Symbol | Exponent | Prefix | Symbol | Exponent |
|---|---|---|---|---|---|
| yotta | Y | 1024 | yocto | y | 10-24 |
| zetta | Z | 1021 | zepto | z | 10-21 |
| exa | E | 1018 | atto | a | 10-18 |
| peta | P | 1015 | femto | f | 10-15 |
| tera | T | 1012 | pico | p | 10-12 |
| giga | G | 109 | nano | n | 10-9 |
| mega | M | 106 | micro | µ | 10-6 |
| kilo | k | 103 | milli | m | 10-3 |
| hecto | h | 102 | centi | c | 10-2 |
| deca | da | 101 | deci | d | 10-1 |
When solving problems with derived units it is recommended to write such quantities in terms of the the base units and carry along the units. This is known as the factor label method or dimensional analysis.
EXAMPLE 0.1
A 180.0 kg sample of chemical Δ has a volume of 140.0 L. Compute the density of chemical Δ in g/cm3.
SOLUTION
First let's get the number of grams:
180.0 kg X [103 g/kg] = 180.0 X 103 g of chemical Δ
Note that the units are treated as algebraic quantities and since [kg/kg] = 1, the kg units are said to cancel.
For the volume,
140.0 L X [ 103 cm3/L] = 140.0 X 103 cm3 of chemical Δ
And the density,
ρ of chemical Δ = [180.0 X 103 g] / [140.0 X 103 cm3] = 1.286 g/cm3
EXAMPLE 0.2
Compare the volumes of three spheres of equal mass but made of different materials: lead ρ = 11.3 g/cm3, silver ρ = 10.5 g/cm3, and aluminum ρ = 2.7 g/cm3.
SOLUTION
Let's take a look at the density formula,
ρ = Mass / Volume
*With the volume constant, mass is directly proportional to the density.
*With the mass constant, volume is inversely proportional to the density.
And volume of a sphere is given by,
Vsphere = [4/3] π r3 = [1/16] π d3
The spheres (drawn to scale) would look like this,
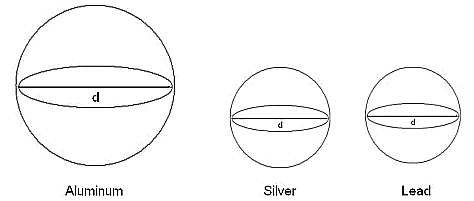
The formulas are not actually required, just know that volumes of high density materials are heavier than equivalent volumes of low density materials. Because the density of silver (10.5 g/cm3) is comparable to the density of lead (11.3 g/cm3), the two spheres have nearly the same volume. Since the density of aluminum is a lot smaller than both silver and lead, the aluminum sphere is a lot larger.
EXAMPLE 0.3
The "G temperature scale" has been calibrated so that,
0 0G = -11.5 0C
100 0G = 197.60C
Draw a thermometer that uses the G scale. Compute the freezing point of water in 0G (G degrees) and convert 150.0 0G to its equivalent in 0C.
SOLUTION
The G scale:

There are [197.6 -(-11.5)] = 209.1 0C between 0 and 100 0G, so the conversion factor in terms of magnitude will be:
1 0G = [100 0C] / [209.1 0G]
The 0C scale is -11.5 at 0 0G,
0C to 0G <-- add 11.5
0G to 0C <-- subtract 11.5
Note that the order in which the operations are performed will change the final answer!
For the freezing point of water,
{[100 0C] / [209.1 0G]} X [00C + 11.5] = 5.50 0G
For the conversion of 150 0G --> 0C,
{[150.0 0G X 209.1 0C] / [100.0 0G]} - 11.5 = 302.2 0C
EXAMPLE 0.4
The Fahrenheit temperature scale has been calibrated so that,
32 0F = 0 0C
212 0F = 1000C
Convert the normal body temperature (98.6 0F) to its equivalent in 0C and the melting point of Nitrogen (-345.8 0F) to their equivalent in 0F.
SOLUTION
There are [212 - 32] = 180 0F between 0 and 100 0G, so the conversion factor in terms of magnitude is:
1 0F = [100 0C] / [180 0F]
The 0C scale is 0 at 32 0F,
0F to 0C <-- add 32
0C to 0F <-- subtract 32
Note that the order in which the operations are performed will change the final answer!
For the normal body temperature,
{[100 0C] / [180 0F]} X [98.6 0F - 32] = 37.0 0C
For the boiling point of Nitrogen,
{[180 0F X -209.9 0C] / [100 0C]} + 32 = 345.8 0F
EXAMPLE 0.5
Due to unsettled differences with France, the United States of America decides to make its own length/mass standard in the form of a Titanium-Nickel alloy bar. The longest edge of the bar will be the meter standard and has been measured to be 1.000000 m. The width and height of the bar are 0.015000 m and 0.010000 m respectively. The mass of the bar is 1.00000 kg and will be the kg standard. Calculate the percent Titanium by mass in the bar. The density of Titanium is 4.51 g/cm3 and the density of nickel is 8.90 g/cm3. Assume volume additivity.
SOLUTION
Volume of alloy bar = 100 cm X 1.50 cm X 1.00 cm = 150 cm3 = 150 mL
Note that 1 mL = 1 cm3 so we can use either unit of volume.
Density of alloy bar = ρ = 1000 g / 150 mL = 6.67 g/mL
ρ = M / V --> V = M / ρ --> Total M / Average ρ = [M1 / ρ1] + [M2 / ρ2]
This means that the mass of Titanium plus the mass of Nickel has to equal the mass of the alloy, here 1000 g. It is simpler to set this value equal to 1 g, we could use 1000 g and still get the same answer because we are working with relative values.
1000 g --> 1 g
M = 1 g = Total mass --> M1 = &Psi = mass of Titanium and M2 = (1–Ψ) g = mass of Nickel
1 g / 6.67 g/mL = [Ψ g / ρ1] + [(1-Ψ) g / ρ2]
1 g / 6.67 g/mL = [Ψ g / 4.51 g/mL] + [(1-Ψ) g / 8.90 g/mL]
The grams cancel and the Lowest Common Denominator is (4.51 X 8.90)
0.150 mL X (4.51 X 8.90) = [{Ψ X (4.51 X 8.90)} / (4.51) mL-1] + [{(1-Ψ) X (4.51 X 8.90)} / (8.90) mL-1]
6.02 mL = [(Ψ X 8.90) mL] + 4.51 mL – [(Ψ X 4.51) mL]
6.02 mL - 4.51 mL = [(Ψ X 8.90) mL] – [(Ψ X 4.51) mL]
1.51 mL = Ψ X 4.39 mL --> 1.51 mL / 4.39 mL = Ψ = 0.344
% Titanium by mass = 34.4 %
EXAMPLE 0.6
One liter (1.00 L) of an ethanol-water solution (commonly known as Vodka) weights 900.0 grams. Ethanol has a density of 0.789 g/cm3 and water has a density 1.00 g/cm3. Compute the percent ethanol by mass in the solution. Assume volume additivity.
SOLUTION
Can be solved in a similar way as problem 1.5. Volume additivity means that the volume of Vodka equals the volume of ethanol plus the volume of water. This is not always true and some substances have either positive or negative partial volumes. Ethanol is an example, but drunks and bartenders don't know that or choose to ignore the fact so we will do the same.
Mass of water = Ψ
Mass of ethanol = 1 - Ψ
Volume of water = 1.00 L X [1.00 X 103 cm3/1.00 L] = 1.00 X 103 cm3
Average density = 900 g / [1.00 X 103 cm3] = 0.900 g/cm3
0.900 g/cm3 = 1.00 g/cm3 (Ψ) + {0.789 g/cm3 X (1 - Ψ)}
0.900 g/cm3 = 1.00 g/cm3 (Ψ) + 0.789 g/cm3 - 0.789 g/cm3 (Ψ)
0.900 g/cm3 = 0.789 g/cm3 - 0.211 g/cm3 (Ψ)
Put Ψ's on one side, plain numbers on the other,
0.111 g/cm3 = 0.211 g/cm3 (Ψ)
[0.111 g/cm3]/[0.211 g/cm3] = Ψ
0.526 = Ψ <-- mass of water (relative amount)
0.526 - Ψ = 0.474 <-- mass of ethanol (relative amount)
water = 52.6 %, ethanol = 47.4 %
EXAMPLE 0.7
In light of the oil crisis, the Saudis are using some type of beer-powered dromedary transport (single hump camel) as an alternative the standard fossil fuel powered transport (car). Certain camel has a beer capacity of 50.0 L and burns 2.75 kg of beer (ρ = 0.795 g/cm3) per kilometer of travel. How far can this camel go in a full hump?
SOLUTION
Camel's hump capacity in cm3 = 50.0 X [103 cm3/L] = 50.0 X 103 cm3
Mass of beer = 50.0 X 103 cm3 X 0.795 g/cm3 = 39.8 X 103 g = 39.8 kg
Distance the camel can travel in a full hump of beer = [39.8 kg] / [2.75 kg/km] = 14.5 km
Note that camels do not store beer in their humps as this problem suggests. Their humps are a reservoir of fatty tissue, while beer is stored in their blood. This allows them to survive days on end without food and water. Our apologies to the dromedary folks out there.
0.2 - Significant digits
You might have noticed that the answers in the previous section have been rounded off to a certain number of significant digits because experimental measurements are inaccurate to some extent. In Example 1.5 the number of significant digits for the mass and dimensions of the alloy bar are indicative of the high degree of certainty required to make an object that is to be used as a standard. Such an object would have to be ground down and measured with high precision calipers to within a certain tolerance. As a rule, there is an uncertainty of one unit in the last significant digit unless otherwise specified. So the number 1.000000 m is automatically assumed to mean 0.999999 or 1.000000 or 1.000001 m.
Thus when rounding off numbers:
-If the digit to the immediate right is 5,6,7,8, or 9, add 1 to the place we are rounding to.
-If the digit to the immediate right is 1,2,3, or 4, simply eliminate that digit.
And for the number significant digits:
-All non-zero digits are significant.
[911 = 3 significant digits]
-Zeros between non-zero digits are significant.
[22.409 = 5 significant digits]
-Zeros to the left of the first non-zero digit are not significant.
[2.02 = 3, 0.25 = 2, 0.025 = 2 significant digits]
-If a number ends in zeros to the right of the decimal point, those zeros are significant.
[2.0 = 2, 2.00 = 3 significant digits]
-If a number ends in zeros to the left of the decimal point, those zeros may or may not be significant.
[110, if written as 11.0 X 101 = 2, if written as 1.10 X 102 = 3 significant digits]
The last two rules seem complicated but they are not. It is only a question of accuracy, which is part of day to day activities in the chemistry laboratory.
When multiplying or dividing numbers, the result of your calculation has the same number of significant digits as the operand with the fewest number of significant digits.
For example:
1.87 X 3.0 = 5.6
1.87 (3 significant digits) X 4.0 (2 significant digits) = 5.6 (2 significant digits)
When adding or subtracting numbers, keep the fewest number of decimal places that are in all of the numbers. Keep in mind that the total number of significant digits is irrelevant.
For example:
5.67 + 6.5432 = 12.21
5.67 (2 decimal places) + 6.5432 (3 decimal places) = 12.21 (2 decimal places)
17.089 - 10.2200 = 6.869
17.089 (3 decimal places) + 10.2200 (4 decimal places) = 6.869 (3 decimal places)
When taking the logarithm of a number, the number of decimal places in the result must be the same as the number of significant digits in the number you started with.
For example:
log10(24) = 1.38
Because 24 has two significant digits, 1.38 has two decimal places. The digits to the left of the decimal point in a logarithm reflect the value of the exponent of the argument of the logarithm expressed in scientific notation. These digits do not contribute to the significant digits of either the argument or the logarithm. The digits to the right of the decimal point in a logarithm reflect the significant digits of the mantissa of the argument. So if you write 24 as 2.4 X 101, the logarithm is:
log10(2.4 X 101) = (0.38) + (1) = 1.38.
If you write 24000 as 2.40 X 104, the logarithm is:
log10(2.40 X 104) = (0.380) + (4) = 4.380.
Notice that 2.40 X 104 has three significant digits, hence the term 0.380, and the 4 comes from the exponent and is thus irrelevant to the number of significant digits retained
Keep in mind that those rules apply to measured quantities which are non-exact. If a number is exact then there is no uncertainty and the number of significant digits is infinite. For example people, with the exception of half-wits, come in integer numbers so there can be either 10 or 11 people but not 10.5.
|
1.1 - History of Atomic Structure
The search for the atom began as a philosophical question. It was the natural philosophers of ancient Greece that began the search for the atom by asking such questions as What is stuff composed of? What is the structure of material objects? Is there a basic unit from which all objects are made?
As early as 400 B.C., some Greek philosophers proposed that matter is made of indivisible building blocks known as atomos. (Atomos in Greek means indivisible.)

Democritus having an argument about atoms
To these early Greeks, matter could not be continuously broken down and divided indefinitely. Rather, there was a basic unit or building block which was indivisible and foundational to its structure. This indivisible building block of which all matter was composed became known as the atom.
We can't base our model on actual observations of atoms, because they are too small to be seen with our most sensitive instruments. Instead, we must come up with a model of an atom that can account for and explain observations that we can actually see. As new observations are made, we are forced to update our model to accommodate them. As a result, our model of the atom has evolved over time, and we must accept the fact that it is likely to change again in the future.
Boyle's studies (middle to late 1600s) of gaseous substances promoted the idea that there were different types of atoms known as elements. Dalton (early 1800s) conducted a variety of experiments to show that different elements can combine in fixed ratios of masses to form compounds. Dalton subsequently proposed one of the first theories of atomic behavior which was supported by actual experimental evidence.
English scientist J.J. Thomson's cathode ray experiments (end of the 19th century) led to the discovery of the negatively-charged electron and the first ideas of the structure of these indivisible atoms. Thomson proposed the Plum Pudding Model, suggesting that an atom's structure resembles the favorite English dessert - plum pudding. The raisins dispersed amidst the plum pudding are analogous to negatively charged electrons immersed in a sea of positive charge.
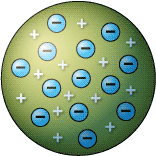
The 'Plum Pudding' model of the atom
This model was soon replaced. In 1911, Ernest Rutherford suggested that his students Geiger and Marsden fire alpha particles (produced by some naturally radioactive materials) at a thin gold foil. They observed that some of the alpha particles were scattered through large angles, indicating that the positive charge in the atom was concentrated in a small volume – the nucleus.
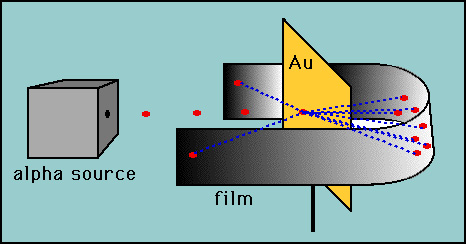
The "gold foil" experiment
Rutherford was forced to discard the Plum Pudding model and reasoned that the only way the alpha particles could be deflected backwards was if most of the mass in an atom was concentrated in a nucleus. Rutherford subsequently proposed a model of atom based on a central nucleus of positive charge circled by negative electrons – like planets orbiting the sun.
Rutherford's model of the atom
1.2 - Nucleus and electrons
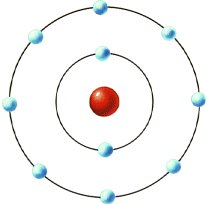
Neils Bohr (1913) improved upon Rutherford's nuclear model by explaining that the electrons present were present in orbits outside the nucleus. The electrons were confined to specific orbits of fixed radius, each characterized by their own discrete levels of energy. While electrons could be forced from one orbit to another orbit, it could never occupy the space between orbits.
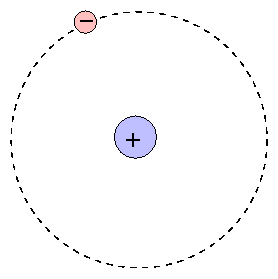
The Bohr Model of the atom
The Bohr model provides a simple, easily remembered picture of the structure of an atom. At the center is the positive nucleus, around which electron(s) move in circular orbits. The farther the electron is from the center, the higher the energy of the atom. Atoms can move from one energy state to another by absorping or emitting a photon, or by colliding with another atom or molecule. However, they are bound to jump between certain very specific energy levels or electron shells.
The first electron shell is closest to the nucleus. It can hold up to two electrons. The second electron shell can hold up to eight electrons and the third electron shell can hold anywhere from eight to 18 electrons and so on. Electrons fill the electron shells closest to the nucleus first, and then fill the outer shells accordingly. For example, an atom of Hydrogen (H) with one electron has its electron in the first electron shell. An atom of Helium (He) has two electrons that are both found in the first electron shell. An atom of Lithium (Li) has three electrons, two of which are in the first shell, and the third going into the second electron shell.
What is the significance of an electron shell being filled? When an electron shell is filled the atom is stable or non-reactive. Let's consider atoms of the elements Hydrogen and Helium. Hydrogen, with only one electron in the first shell, is very reactive. It is highly flammable. However, Helium, with two electrons in the first electron shell, is non-reactive. It is called an inert gas.
In addition to mass, subatomic particles also have charges. Electrons have a charge of negative one, and protons have a charge of positive one. These positive and negative charges are opposite and exactly equal in strength. For this reason, an atom with one electron and one proton has no net charge. The +1 charge of the proton and the -1 charge of the electron cancel each other out. Neutrons, as their name suggests, are neutral, or uncharged particles. Neutrons contribute mass, but no charge to an atom.
Atoms of elements must always have the same number of electrons and protons or the elements would be highly reactive and very unstable. If an atom has an unequal number of electrons or protons, it is an ion. Ions can exist only when surrounded by other ions of opposite charge.
|
||
|
Proton |
Neutron |
Electron |
|
In nucleus Tightly Bound Positive Charge Massive |
In nucleus Tightly Bound No Charge Massive |
Outside nucleus Weakly Bound Negative Charge Not very massive |
1.3 - Introduction to Quantum Theory
Although the Bohr model adequately explained how atomic spectra worked, it failed in many levels:
...
1.4 - The Periodic Table
The periodic table of the elements not only supplies information about the numbers of protons, electrons, and neutrons, but also predicts the reactivity of the atoms of each element. This allows us to predict how different elements will combine to form compounds. The electrons in atoms interact and form chemical bonds to make different compounds with unique properties. Compounds are formed when the atoms of different elements combine through the sharing of their electrons or the interaction of their charges.
The periodic table supplies the information we will need to decipher what the molecular formula of a compound represents, and also how to predict the proportions of elements in a compound. The periodic table contains the following information:
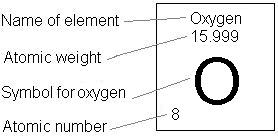
Periodic Data for Oxygen
...
|
All matter such as solids, liquids, and gases, is composed of atoms. Atoms are almost always grouped together with other atoms to form what is called a molecule. Only a few gases such as helium are composed of individual atoms as the structural unit. Therefore, the molecule is considered to be the basic building block of matter.
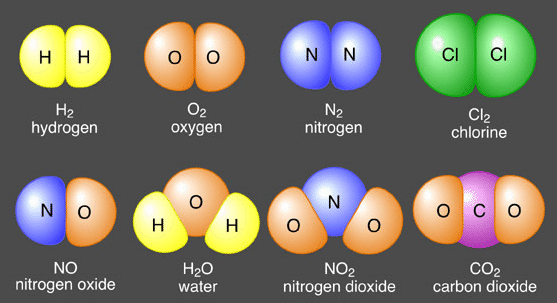
Some common molecules
2.1 - Ionic Bonds
...
2.2 - Covalent Bonds
The covalent bond is the strongest chemical bond. These bonds allow for the formation of stable compounds and satisfy the need for atoms to have a filled outer electron shell. When atoms share electrons they actually get close enough that their electron shells overlap. In this way electrons from two or more atoms can share their electrons and form stable molecules.
2.3 - Molecular Shape
...
|
3.1 - ...
...
|
4.1 - ...
|
5.1 - ...
|
7.1 - ...
|
8.1 - ...
[1] Biddle, V., Parker, G., Chemistry | Precision & design, Second Edition, Pensacola, Florida, 2000.
[2] Focus on Earth Science: Laboratory Manual. Upper Saddle River, New Jersey: Prentice-Hall Inc., 2001.
[3] Inquiry Skills Activity Book. Upper Saddle River, New Jersey: Prentice-Hall, Inc., 2001.
[4] Project Earth Science: Physical Oceanography. Arlington, VA.: National Science Teachers Association, 1995.