5TH Grade Mathematics [Arithmetic Level 1] |
|
|--Introductory Concepts
|--Addition
|--Subtraction
|--Multiplication
|--Division
|--Exponents
|--Scientific Notation
|--Order of operations
|--Numerator and Denominator
|--Changing the type of a fraction
|--Multiplying/Dividing fractions
|--Adding/Subtracting fractions
|--Linear Measures
|--Volume
|--Mass
|--Angles
|--Triangles
|--Other Polygons
Required Textbook: A Beka Arithmetic 5, Work-Text, Pensacola, Florida, current edition.
[a] Solve problems, compute fluently, and make reasonable estimates.
[i] Select appropriate methods and tools for computations (e.g., mental computation, estimation, calculators, paper and pencil).
[ii] Explain why one from of a number might be more useful for computation than another form.
[iii] Add, subtract, multiply, and divide whole numbers and decimals.
[iv] Use models, benchmarks, and equivalent forms to add and subtract commonly used fractions with like and unlike denominators.
[v] Solve real-world problems using decimals, fractions, and percents.
[vi] Represent and analyze patterns, relations, and functions.
[vii] Generalize and extend geometric and numerical patterns.
[viii] Represent and analyze mathematical situations and structures using algebraic symbols.
[ix] Demonstrate understanding that an equation is a number sentence stating two quantities are equal.
[b] Illustrate general properties of operations.
[i] Apply commutative, associative, zero, distributive, and identity properties.
[ii] show that division is not commutative.
[iii] Develop an understanding of geometric concepts and relationships as the basis for geometric modeling and reasoning to solve problems involving one-, two-, and three-dimensional figures.
[iv] Use the attributes of geometric figures to develop definitions.
[v] Draw points, lines, line segments, rays, and angles.
[vi] Identify and describe the attributes of a circle using appropriate mathematical language (e.g., radius, diameter, center).
[vii] Investigate and describe the results of subdividing and combining geometric figures.
[viii] Compare and contrast congruent and symmetrical geometric figures.
[ix] Describe characteristics of lines and angles (e.g., parallel, perpendicular, intersecting, right, acute, obtuse).
[x] Describe location and movement using appropriate mathematical language (Quadrant I, II...) of a coordinate system.
[c] Use visualization, spatial reasoning, and geometric modeling to solve problems.
[i] Construct and draw two- and three-dimensional geometric figures.
[ii] Create and describe mental images of objects, patterns, and paths;
[iii] Build a three-dimensional object from a two-dimensional representation (nets) of that object and use visualization and spatial reasoning to solve real-world problems.
[iv] Understand measurable attributes of objects and the units, systems, and processes of measurement.
[v] Demonstrate understanding of the concepts of length, perimeter, circumference, area, weight, capacity, volume, elapsed time, and angle measure;
[vi] Demonstrate understanding that measurements are approximations, how differences in units affect precision.
[vi] Demonstrate understanding of the relationships among the units within the same system of measurements.
[d] Understand and apply basic statistical and probability concepts as they, organize, and analyze data, and to make predictions and conjectures.
[i] Collect data using observations, surveys, and experiments and understand how data-collection methods affect the nature of the data set.
[ii] Represent data using pictographs, bar graphs, tables, circle graphs, and line graphs. Interpret data displayed in pictographs, bar graphs, tables, circle graphs, and line graphs.
[iii] Select and use appropriate statistical methods to analyze data. Use measures of central tendency (i.e., mean, median, mode).
[iv] Understand and apply basic concepts of probability.
[v] Describe the likelihood or chance of events as likely, unlikely, certain, equally likely, or impossible using a sample space to predict the probability of an event.
[vi] Understand that the measure of the likelihood of an event can be represented as a number from 0-1
0.1 - Numbers
The 300 Spartans, is a 1962 war film depicting the Battle of Thermopylae. There is a scene where a spy tells the Spartan king Leonidas that the Persian army is so numerous that he ran out of numbers while counting them. Does this statement makes sense?
Let's start by defining a cardinal number, this is the number of elements in a set. For example, the cardinal number of the empty set is 0 and the cardinal number of the set of natural numbers up to and including 20 is 20. The question is: what the cardinal number of the set of all natural numbers? In other words, how many natural numbers are there? You can try counting to 1,000,000,000 and beyond, probably count yourself to death and there is always a number greater than any given number. The natural numbers (also known as the positive integers, or counting numbers) are infinite in number. Thus it is very unlikely that the spy ran out of numbers, actually he was captured and stopped counting at that point.
The set of positive integers just mentioned is customarily written
where N stands for Natural. These can be arranged in a manner such that, given part of the list, we can say what the next number on the list will be. The (...) stands for continuity. Because the cardinal number of all natural numbers is infinity, you can never run out of numbers to count fingers, toes, apples, people...
There are also integers that have a negative sign, you cannot use these to count things, so they are not part of the Natural number set. The set of integers (denoted by Z), is the union of the set of the positive integers, the set of the negative integers, and zero. Let's put the integers in a one-to-one correspondence with the natural numbers:
N Z 1 <---> 0 2 <---> 1 3 <---> -1 4 <---> 2 5 <---> -2 6 <---> 3 7 <---> -3 . . .At this point it looks like there are more integers (Z) than natural numbers (N). But let's have a look at Hilbert's Hotel,
Hilbert's Hotel, named after mathematician David Hilbert, is a hotel with an infinite number of rooms. Imagine that every single one of them is occupied. What does the manager do when someone else shows up and wants a room? He doesn't need to turn that person away. Instead, he just moves the person in room 1 into room 2, the person in room 2 into room 3, the person in room 3 into room 4, and so on. Room 1 is now vacant for the new guest. Now, a hundred new guests appear. The manager now moves the guest in room 1 into room 101, the guest in room 2 into room 102, etc. and thus creates room for the 100 guests.
Now an infinite number of people show up, all wanting rooms. What does the manager do now? He simply moves the person in room 1 into room 2, the person in room 2 into room 4, the person in room 3 into room 6, and in general the person in room n into room 2n. Now there are an infinite number of rooms free (all of the odd-numbered rooms) for this infinite group of people.
Hilbert's Hotel is paradoxical, but it illustrates an interesting property of infinite sets: An infinite set can be put in one-to-one correspondence with an infinite subset of itself. It also illustrates the seemingly impossible situations that become possible when dealing with infinity.
The set rational numbers (Q) is infinite as well,
N Q
1 0/1
2 1/1
3 1/2
4 2/1
5 1/3
6 3/1
7 1/4
. . .
0.2 - Place-value system
Place value, is the particular power of the base of a counting system that is represented by a particular position in a place-value notation. For example, units, tens, hundreds, etc. in the decimal system, so that in 647 the place-value of the 4 is 10.
In our decimal number system, the value of a digit depends on its place, or position, in the number. A number in standard form is separated into groups of three digits each. Each of these groups is called a period. Beginning with the ones place at the right, each place value is multiplied by increasing powers of 10. For example, the value of the first place on the right is "one", the value of the place to the left of it is "ten," which is 10 times 1. The place to the left of the tens place is hundreds, which is 10 times 10, and so forth.
The zero and the counting numbers (1,2,3,...) make up the set of whole numbers. But not every number is a whole number. Our decimal system lets us write numbers of all types and sizes, using a clever symbol called the decimal point. As you move right from the decimal point, each place value is divided by 10.
123 456 789 . 123 ||| ||| ||| | ||| ||| ||| ||| | |||__ Thousandths ||| ||| ||| | ||___ Hundredths ||| ||| ||| | |____ Tenths ||| ||| ||| | ||| ||| ||| |______ Decimal Point ||| ||| ||| ||| ||| |||__ Ones ||| ||| ||___ Tens ||| ||| |____ Hundreds ||| |||______ Thousands ||| ||_______ Ten Thousands ||| |________ Hundred Thousands |||__________ Millions ||___________ Ten Millions |____________ Hundred Millions
0.3 - Introduction to fractions and decimals
Consider an area of arable land, lets say 1 acre.
| .
. 1
acre
of arable land
|
Now you are told that mom wants to plant corn in 4/10 of the land. Picture the 1 acre of land divided into 10 equal parts. Four of those parts are for planting corn.
| . | . |
| . | . |
| . | . |
| 1/10 or 0.1 for corn |
1/10 or 0.1 for corn |
| 1/10 or 0.1 for corn |
1/10 or 0.1 for corn |
1/10 + 1/10 + 1/10 + 1/10 = 4/10 of an acre for planting corn
0.1 + 0.1 + 0.1 + 0.1 = 0.4 of an acre for planting corn
Now your mom wants to use 1/2 of the land for planting beans and a pig sty will be built in the ramaining land.
The number of 1/10 pieces that make up 1/2 of the acre are,
1/10 + 1/10 + 1/10 + 1/10 + 1/10 = 5/10 = 1/2
Now you have used up 5/10 of an acre to plant beans and 4/10 to plant corn, that leaves,
1 - 4/10 - 5/10 = 1/10
So you have one tenth (1/10) of an acre to build the pig sty. Let's put it in upper right the corner.
| 1/10 or 0.1 for pig sty |
1/10 or 0.1 for beans |
| 1/10 or 0.1 for beans |
1/10 or 0.1 for beans |
| 1/10 or 0.1 for beans |
1/10 or 0.1 for beans |
| 1/10 or 0.1 for corn |
1/10 or 0.1 for corn |
| 1/10 or 0.1 for corn |
1/10 or 0.1 for corn |
You might have noticed that a decimal is another way to write a fraction. In $1.25 , $0.25 is part of a dollar. It is 25/100 or 5/20 (or one quarter). In a decimal, the farther right the number the smaller it's value. As you already know, our number system is a base 10 system. This means you can change the place value of the number by one spot in a period by either multiplying or dividing by 10.
For example:
$0.25 X 10 = $2.50
25/100 X 10 = 2.50
The decimal point moved one place to the right because you multiplied by 10.
$2.50 X 1/10 = $0.25
2.50 X 1/10 = 25/100
The decimal point moved one place to the right because you divided by 10.
|
1.1 - Addition
Addition operations are denoted by the + sign. Combining two minus sigs gives plus [ - (-) = +]. The addition operator (plus sign) will take any two numbers, called addends, as operands to work on. The result is called the sum of the two numbers. The operation of addition is commutative. This means that the addition of two numbers will give the same sum regardless of the order in which the numbers are added.
Another property of addition is associativity, which comes up when one tries to define repeated addition.
For example:
(2 + 4) + 6 = 2 + (4 + 6)
If one adds zero to any number, the quantity won't change,
1 + 0 = 1, 1000 + 0 = 1000
Thus, zero is the identity element for addition, also known as the additive identity.
Mental addition in the decimal system is the internalization of addition facts from a hundreds board,
+ | 1 2 3 4 5 6 7 8 9 10
--+---------------------------------------
10 |11 12 13 14 15 16 17 18 19 20
| ^
20 |21 22 23 24 25 26 27 28 29 30 |
| |
30 |31 32 33 34 35 36 37 38 39 40 subtract 10
| |
40 |41 42 43 44 45 46 47 48 49 50 |
| <--subtract 1 -------- add 1-->
50 |51 52 53 54 55 56 57 58 59 60 |
| |
60 |61 62 63 64 65 66 67 68 69 70 add 10
| |
70 |71 72 73 74 75 76 77 78 79 80 |
| v
80 |81 82 83 84 85 86 87 88 89 90
|
90 |91 92 93 94 95 96 97 98 99 100
One could memorize all the facts, but other strategies are more efficient:
-One through nine: Use your fingers or toes.
-Zero is the additive identity, adding zero is trivial.
-Tens: increase the tens place; 22 + 10 = 32, 35 + 50 = 85
-Separate ones, tens , hundreds... In the hundreds board above, you would add ones by moving across the board and add tens by moving down the board.
To add multidigit numbers, one typically aligns the addends vertically and adds the columns, starting from the ones column on the right. If a column exceeds ten, the extra digit is carried into the next column.
For example:
1234 |add 4 + 8
+5678 <----|the answer is 12
-------
1 <----|carry the 1
1234
+5678
-------
2 <----|write the 2
1
1234 |add 3 + 7
+5678 <----|the answer is 10, add the 1 you carried, the answer is 11
-------
2
11 <----|carry the 1 (the second to the right)
1234
+5678
-------
12 <----|write the two
11
1234 |add 2 + 6
+5678 <----|the answer is 8 add the 1 you carried, the answer is 9
-------
12
11 <----|no number to carry this time because 9 has only one digit
1234
+5678
-------
912 <----|write the nine
11
1234 |add 1 + 5
+5678 <----|the answer is 6
-------
6912 <----|write the six and you are done
The same procedure can be extended to numbers with decimals,
123.45
+678.9
---------
|
|_______note the decimal point
123.45
+678.9
---------
5
1
123.45
+678.9
---------
.35
11
123.45
+678.9
---------
2.35
111
123.45
+678.9
---------
802.35
Note that the decimal points in the addends must be aligned.
1.2 - Subtraction
Subtraction uses the minus (-) sign. The generic subtraction operator will take any two numbers as operands. The result is called the difference of the two numbers. The subtraction procedure is the opposite of addition in every way,
For Example:
984 <----|subtract 6 from 4? cannot be done
-546 |borrow 1 from the tens place, 4 becomes 14
------
8 becomes 7
|4 becomes 14
||
984 <----|subtract 6 from 14
-546
------
8 <----|the answer is 8
984 <----|subtract 4 from 7
-546 |no need to borrow from the hundreds place
------
38 <----|the answer is 3
984 <----|subtract 5 from 9
-546
------
38 <----|the answer is 4 and you are done
Sometimes you might need to borrow from a number and it turns out to be zero (0), then you need to go to the next place in the number system.
For example:
1 0 0
- 9 9
------
We can't subtract 9 from 0, so we go to the tens place to borrow a ten. Since
there are no tens to borrow, we have to go to the hundreds place to borrow a hundred.
Since there is only a 1 in the hundreds place, this turns into a zero,
0 10
/ /
1 0 0
- 9 9
------
Now we can take one from the tens, turning the 0 into 10 ones, from which we can subtract 9,
0 9 10
/ / /
1 0 0
- 9 9
------
1
Finally, we can subtract the 9 tens,
0 9 10
/ / /
1 0 0
- 9 9
------
0 0 1
The 9 in the tens place came from the 10 tens we borrowed from one hundred), minus the 1 ten that was borrowed
from it by the ones place.
Try adding:
99
+ 1
----
and 9 in the tens place will turn into a 10.
Subtraction is not a commutative operation. Changing the order of the operands will likely give a different result.
1.3 - Multiplication
Multiplication is denoted by an asterisk (*), X, or (•) sign. However, the X sign is normally not used in algebra, and is instead limited to very basic elementary math, as it can easily be confused with an "x" variable. The generic multiplication operator will take any two numbers, called factors, as operands. The result is called the product of the two numbers. If the multiplicants are not both written as numbers, the multiplication sign can be left out. Thus, the following example expressions are equivalent:
3*a*b = 3 X a X b = 3(a*b) = 3(a X b) = 3(ab) = 3ab Multiplication is a form of repeated addition. For example:
3 X 5 means 3 + 3 + 3 + 3 + 3 or 5 + 5 + 5
For integers, fractions, real and complex numbers, multiplication has certain properties:
The commutative property: the order in which two numbers are multiplied does not matter,
a X a = b X a
The associative property means that for any three numbers a, b, and c,
(a X b)c = a(b X c)
Note that the parentheses mean that the operations inside the parentheses must be done before anything outside the parentheses is done.
Multiplication also has what is called a distributive property with respect to the addition,
a(b + c) = ab + ac
Also of interest is that any number times 1 is equal to itself, thus,
1 X a = a
this is called the identity property. In this regard the number 1 is known as the multiplicative identity.
Multiplication by of zero is zero,
a X 0 = 0
no matter what "a" is as long as it is a finite quantity.
Multiplication with negative numbers requires care. Consider negative five multiplied by positive five,
-5 X 5 = -25
Thus negative times positive gives a negative.
Now, consider negative five multiplied by negative five,
-5 X -5 = 25
Thus negative times negative gives a positive. In conclusion, multiplication of equal signed numbers (both negative or both positive) gives positive, while multiplication of different signed numbers (one positive and one negative) gives negative. A slightly more advanced way of saying this is:
Multiplication by a positive number preserves order: if a > 0, then if b > c then ab > ac
Multiplication by a negative number reverses order: if a < 0, then if b > c then ab < ac
Other mathematical systems that include a multiplication operation may not have all these properties. For example, multiplication is not, in general, commutative for matrices and quaternions. But this is something for more advanced students to worry about.
The standard methods for multiplying numbers using pencil and paper require a multiplication table of memorized or consulted products of small numbers. Typically any two numbers from 0 to 9 are enough. Here is a MULTIPLICATION TABLE for the facts 1-12...
x | 2 3 4 5 6 7 8 9 10 11 12
--+------------------------------------------
2 | 4 6 8 10 12 14 16 18 20 22 24
|
3 | 6 9 12 15 18 21 24 27 30 33 36
|
4 | 8 12 16 20 24 28 32 36 40 44 48
|
5 |10 15 20 25 30 35 40 45 50 55 60
|
6 |12 18 24 30 36 42 48 54 60 66 72
|
7 |14 21 28 35 42 49 56 63 70 77 84
|
8 |16 24 32 40 48 56 64 72 80 88 96
|
9 |18 27 36 45 54 63 72 81 90 99 108
|
10 |20 30 40 50 60 70 80 90 100 110 120
|
11 |22 33 44 55 66 77 88 99 110 121 132
|
12 |24 36 48 60 72 84 96 108 120 132 144
Here rows and columns are headed by the numbers to multiply, and the entry in each cell is the product of the column and row headings. If you want to multiply 7 X 9 just look up where the 7 in the main (black) row intercepts the 9 in the main column. The row and the column meet at 63 and that is your answer. If you consider yourself a decent if not good student of mathematics, it is essential that you memorize the multiplication table for the facts 0-9.
With a single digit multiplier the procedure is straightforward,
1 <--| 3 X 6 = 18
9876 X 3 | write the 8 (unit) and carry the 1 (ten) over
----------- |
8 <--|
21 <--| 3 X 7 = 21
9876 X 3 | add the 1 left from previous operation
----------- | 21 + 1 = 22, Note that you add the 1 (ten) to the units
28 <--| write the 2 and carry the 2 over
221 <--| 3 X 8 = 24
9876 X 3 | add the 2 left from previous operation
----------- | 24 + 2 = 26
628 <--| write the 6 and carry the 2 over
221 <--| 3 X 9 = 27
9876 X 3 | add the 2 left from previous operation
----------- | 27 + 2 = 29
29628 <--| write the 29 and you are done
A natural way of multiplying large numbers is by long multiplication: multiply the multiplicand by each digit of the multiplier and then add up all the properly shifted results.
345 X 607
---------------
2415 <-- 345 X 7
000 <-- shift one space to the right, 345 X 0 = 000
2070 <-- shift one space to the right, 345 X 6 = 2070
---------------
209415 <-- add up all results
This has the advantage of being fairly accurate when performed by a skilled person but requires memorization of a multiplication table, neat penmanship and mental focus.
If the multiplier, multiplicand or both contain decimal places, then the procedure is the same except for one extra step.
Count the number of decimal places in the multiplier and the multiplicand,
34.5 X 60.7
| |________ one decimal place in the multiplier
|_______________ one decimal place in the multiplicand
that is two decimal places total
Do the multiplication as if the decimal points were not there,
34.5 X 60.7
---------------
2415 <-- 345 X 7
000 <-- shift one space to the right, 345 X 0 = 000
2070 <-- shift one space to the right, 345 X 6 = 2070
---------------
209415 <--| add up all results
2094.15 <--| shift the decimal point
| by the total number of decimal places
| in the multiplier and the multiplicand
1.4 - Division
Division uses the ÷ sign. It may also be signified by the slash, /, :, or the fraction bar. The generic division operator will take any two numbers as operands. The number before the ÷ sign is called the dividend and the number after the ÷ sign is called the divisor. The result is called the quotient of the two numbers.
6 ÷ 3 = 2 | | |__quotient | |______divisor |__________dividend 6 <--dividend --- = 2 <--quotient 3 <--divisorDivision is not a commutative operation. Switching the dividend and the divisor will likely give a different quotient. For Example:
8 ÷ 2 = 4 and 2 ÷ 8 = 0.25
The division with a divisor of 0 is not defined. There is no answer for it,
9 ÷ 0 = not defined
Note however that the inverse statement is not true,
0 ÷ 9 = 0
Also, just like in multiplication, any number divided by 1 is equal to itself, thus,
a ÷ 1 = a
Long division is a procedure for calculating the division of one integer by another integer to produce a result called the quotient. The procedure converts the problem of dividing a divisor into a large dividend, into a series of divisions of the divisor into smaller numbers.
Example:
Start with the first two digits [54]
4 <-- 12 goes 4 times into 54 and the remainder is 6
_______
548184 )12
-48 <-- Subtract [4 X 12 = 48] from 54
4
_______
548184 )12
-48
68 <-- Bring down the next digit
45 <-- 12 goes 5 times into 68 and the remainder is 8
_______
548184 )12
-48
68
-60 <-- Subtract [5 X 12 = 60] from 68
81 <-- Bring down the next digit
456 <-- 12 goes 6 times into 81 and the remainder is 9
_______
548184 )12
-48
68
-60
81
-72 <-- Subtract [6 X 12 = 72] from 81
98 <-- Bring down the next digit
4568 <-- 12 goes 8 times into 98 and the remainder is 2
_______
548184 )12
-48
68
-60
81
-72
98
96 <-- Subtract [8 X 12 = 96] from 98
24 <-- Bring down the next digit
45682 <-- 12 goes 2 times into 98 and the remainder is 0
_______
548184 )12
-48
68
-60
81
-72
98
96
24
-24 <-- Subtract [8 X 2 = 24] from 24
0 <-- You are done
The procedure can also be extended to include divisors which have a finite or terminating decimal expansion. In this case the procedure involves multiplying the divisor and dividend by the appropriate power of ten so that the new divisor is an integer and then proceeding as normal.
For Example:
________
28 )8
3 <----|8 goes 3 times into 26 and the ramainder is 2
________
28 )8
-24 <----|subtract [3 X 8 = 24] from 26
4
3. <----|add a decimal point
________ |
28 )8 |
-24 |
40 <----|add a 0 to the 4 and make it 40
3.5 <----|8 goes 5 times into 40
________
26 )8
-24
40
-40 <----|subtract [5 X 8 = 40] from 40
00 <----|the remainder is zero, so you are done.
The remainder will not always become zero in a finite number of steps. If you try
________
10 )3
You would get 3.3333333... and never get done with the division. The answer should be truncated after a number of decimals and a bar placed over the last digit to indicate this fact,
_
3.33
________
10 )3
10
10
1
Alternatively, you could write the answer as a mixed number: 3 1/3
1.5 - Exponents
Exponents are shorthand for multiplication, For example:
The exponent stands for how many times the base is being multiplied. The process of using exponents is called raising to a power.
Numbers with exponents that are whole numbers larger than 1 indicate the number of factors to be multiplied, thus that number is multiplied by itself as many times as the exponent shows.
There are a few rules that simplify our dealings with exponents, let's simplify some expressions using these rules,
Simplify (x3)(x2)
(x3)(x2) = x5
which also equals x(3+2). What leads to one of the exponent rules: Whenever you multiply two terms with the same base, you can add the exponents. Note you cannot do the same for (y3)(x2) because the bases are different. This is also true for the division of exponents,
(y3)/(x2) = (y3)/(x2), because different bases cannot combine.
Simplify (x3)/(x2)
(x3)/(x2) = x
what yields another rule: Whenever you divide two terms with the same base, you can subtract the exponents. When dividing different bases, each of them must be raised to its respective power first,
(23)/(32) = 8/9
This does not equal 2/3, which is the answer you would get if you just subtract the exponents.
Simplify (x3)2
(x3)2 = x6
Thus, whenever you have an exponent expression that is raised to a power, you can multiply the exponent and power.
If there is a product inside the parentheses, and a power on the parentheses, then the power goes on each element inside, for example:
(xy3)2 = (xx)(yyy)(yyy) = x2x6
The same rule applies to quotients,
This rule does not work with sum or difference within the parentheses, for example:
If you raise each number within the parentheses to the power of 2 and then add them up, the answer will be different,
This is why it is so important to know the order of operations.
A negative exponent is a quotient with the base in the divisor position. So you need to flip the base from the upper to the lower side, for example:
If the base is multiplied by a number, the number goes in the divident,
One last rule: Anything to the power zero is just "1"
2x0 = 2 X 1 = 2
(x3)0 = 1
(x/y)0 = 1
567800000000000 = 1
You get the idea. But don't ask about 00, let's just say it is an undefined quantity until all mathematicians decide what to do with it.
1.6 - Scientific Notation
Scientific notation is the way that scientists easily handle very large numbers or very small numbers. For example, instead of writing 0.0000000076, we write 7.6 x 10-9. Think of 7.6 x 10-9 as the product 7.6 (the digit term) and 10-9 (the exponential term). The exponent of 10 is the number of places the decimal point must be shifted to give the number in long form. A positive exponent shows that the decimal point is shifted that number of places to the right. A negative exponent shows that the decimal point is shifted that number of places to the left.
Examples:
1 000 000.0 1.000 000 0 |-------| <--the decimal point is shifted 6 places to the right ||| ||| 123 456 Thus, 1 000 000.0 = 1.000 000 0 X 106 0.000 000 10 0.000 000 1.0 |---------| <--the decimal point is shifted 7 places to the left ||| ||| | 123 456 7 Thus, 0.000 000 1 = 1.0 X 10-7 432 000.0 4.32 000 0 |------| <--the decimal point is shifted 5 places to the right ||| || 123 45 Thus, 432 000.0 = 4.32 X 105Note that 4.32 X 105 and 4.320000 X 105 have the same value. The way the number is written depends on the number of significant digits, which means how many digits are good or reflect the value of real data. The concept of significant digits is beyond the scope of this text but let's give an example,
$100.253 $1.00 253 |--| <--the decimal point is shifted 2 places to the right 12 $100.253 = $1.0025 X 102The final answer is one digit short compared to the initial quantity. This is because we can recover a meaningful number without the last digit,
See what happens if you write your tax refund in scientific notation,
$250.25 $2.50 25 |--| <--the decimal point is shifted 2 places to the right 12 $250.25 = $2.50 X 102Let's recover the number,
1.7 - Order of operations
Order of operations are a set of rules that mathematicians have agreed to follow to avoid mass confusion when simplifying mathematical expressions or equations. Without these simple, but important rules, learning mathematics would be maddening. The math community has agreed upon setting up some operations as more important and thus decided that they should always be done first. Here is what they decided:
| 1'st | PARENTHESES | Grouping symbols are always done from the innermost set outward. |
| 2'nd | EXPONENTS | Remember
applying an exponent is different than just multiplying.
Ex: 23 means 2 x 2 x 2 = 8 |
| 3'rd | MULTIPLY | These operations are done in the order they appear from left to right. They are done together because they have the SAME IMPORTANCE. |
| DIVIDE | ||
| 4'th | ADD | Here again we have two operations of the SAME IMPORTANCE. These are done in the order that they appear from left to right. |
| SUBTRACT |
The saying, Please Excuse My Dear Aunt Sally, is often used to help folks remember the proper order. The first letter of each word here stands for a math operation.
| Parentheses | |||
| Exponents | |||
| Multiply or Divide | |||
| Add or Subtract | |||
|
|
|
|
|
| Example 1: | Evaluate 52 x 24 | ||||||||
| Solution: |
|
| Example 2: | Evaluate 289 - (3 x 5)2 | |||||||||
| Solution: |
|
| Example 3: | Evaluate 8 + (2 x 5) x 34 ÷ 9 | ||||||||||||||
| Solution: |
|
|
2.1 - Numerator and denominator
In text, fractions are usually written in a horizontal form, such as "5/112," for ease of reading. When performing calculations, fractions are usually written in a vertical form, such as
5
---
112
The top (or first) number is called the numerator. The number on bottom
(or second number) is called the denominator. In the fraction 5/112, "5" is the numerator
and "112" is the denominator.
2.2 - Changing the type of a fraction
Fractions which can be reduced to a whole number should be reduced. To reduce a fraction to a whole number, divide the denominator into the numerator.
9/3 = 3
8/4 = 2
Any fraction greater than 1 can be reduced either to a whole number or a mixed number. A mixed number contains both a whole number and a fraction. Some fractions can be reduced to a mixed number. To obtain a mixed number, divide the denominator into the numerator.
10/3 = 3 1/3
22/7 = 3 1/7
You can use either an improper fraction or a mixed fraction to show the same amount. For example,
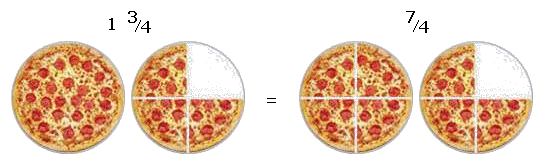
To convert an improper fraction to a mixed fraction, follow these steps:
Example: Convert 11/4 to a mixed fraction
Divide: 11 ÷ 4 = 2 with a remainder of 3
Write down the (2)
__________________
| 3 <------- write down the remainder (3)
+-------------> 2 ---
4 <------- above the denominator (4)
To convert a mixed fraction to an improper fraction, follow these steps:
Example: Convert 3 2/5 to an improper fraction
Multiply the whole number by the denominator: 3 × 5 = 15
Add the numerator to that: 15 + 2 = 17
Write down the (17)
___________________
|
+-------------> 17
---
5 <------- above the denominator (5)
Fractions whose numerator and denominator are divisible by the same digit can be reduced by
dividing both the numerator and denominator by this digit. This does not change the value of the fraction
16/32 = 1/2
The numerator and the denominator are divisible by 2, 4, 8, or 16. Dividing by 16 will give you the lowest equivalent fraction. To review the statement that reducing a fraction does not change its value:
16/32 = 8/16 = 4/8 = 1/2
Remember to reduce all fractions to their lowest terms.
2.3 - Multiplying/Dividing fractions
The multiplication and division functions are relatively simple operations, however, and multiplication must be understood before addition and subtraction of some fractions can be performed.
To multiply fractions:
[1] Multiply the numerators together; [2] Multiply the denominators together; and [3] Place the product of the numerators over the product of the denominators.For example:
2 4 [2 x 4] 8
---- x ---- = ------------ = -----
3 5 [3 x 5] 15
1 2 [1 x 2] 2
---- x ---- = ------------ = -----
3 7 [3 x 7] 21
When you divide a fraction by another fraction, invert (flip) the second fraction and multiply the fractions. For example:
2 4 [2 x 5] 10 5
---- ÷ ---- = ------------ = ----- = ----
3 5 [3 x 4] 12 6
1 2 [1 x 7] 7
---- ÷ ---- = ------------ = -----
3 7 [3 x 2] 6
2.4 - Adding/Subtracting fractions
When you add two fractions with the same denominator, you add the numerators and put the total over the common denominator.
3 4 [3 + 4] 7 5
---- + ---- = ------------ = ----- = ----
3 3 3 3 6
5 2 [5 + 2] 7
---- + ---- = ------------ = ----- = 1
7 7 7 7
As a rule, when working with fractions -- you can't add fractions with different denominators.
This means that, in order for two fractions to be added together, the bottom numbers must be the same.
More than two fractions can be added together at one time as long as
they all have the same denominator,
3 4 3 10
---- + ---- + -------- = -----
3 3 3 3
5 2 4 11
---- + ---- + ------ = -----
7 7 7 7
When you subtract two fractions with the same denominator, you subtract the numerators and put the difference over the common denominator.
9 5 4
---- - ---- = -----
12 12 12
4 2 2
---- - ---- = ------
18 18 18
|
3.1 - Linear measures
Linear units measure in one dimension, such as lenght, width, height, or distance. An important skill you must attain is the ability to decide which linear unit to use in different situations.
For example,

As you can see, some units work better than others depending on the situation. If were asked to write down the distance you walk in one hour using inches, you would end up with a number in the range of thousands,
More Examples,
The width of a magazine is about 8 ____.
It is reasonable to use inches. If we were to use feet, we end up with a measure comparable to the width of a cell in a maximum security prison.
A man's height is about 6 ____.
It is best to use feet. If we use inches, that is like the height of a cat. And 6 yards is like the height of a one story house.
The lenght of a football field is about 100 ____.
We should use yards. If we use miles, we end up with a football field with one end in New York and the other end in some other state. A lenght of 100 feet would be too short for a football field but is still big enough for a basketball court.
Sometimes you will need to change one unit to another. For that you will need to know how much of one unit is contained in another,
12 inches (in) = 1 foot (ft)
3 feet = 1 yard (yd)
5280 feet = 1 mile (mi)
1760 yards = 1 mile
Examples,
1 ft
48 in X ------ = 4 ft
12 in
Here we used the fact that 1 ft = 12 in. These two numbers are put into a conversion factor in such a
way that the units that are not needed will cancel.
3 ft
4 yd X ------ = 12 ft
1 yd
Here we used 3 ft = 1 yd.
5280 ft
2 mi X --------- = 10560 ft
1 mi
Here we used 5280 ft = 1 mi.
1 mi
7040 yd X --------- = 4 mi
1760 yd
Here we used 1760 yd = 1 mi.
3.2 - Volume
If we measure the amount of space occupied by anything that contains matter, we are measuring volume. How much volume something (such as a cup or a box) can hold is called its capacity.
The volumes of solid objects is usually given in cubic units (such as cubic centimeters or cubic feet). For historical reasons, the volume of liquids is usually given in liters, gallons, quarts, and other fluid measures. The table below gives some English and metric volume units.

Within the customary system, the common units for measuring capacity are fluid ounces, cups, pints, quarts, and gallons.
|
|
|
1 cup (c.) |
|
8 fluid ounces (fl. oz.) |
|
1 pint (pt.) |
|
2 cups (c.) |
|
1 quart (qt.) |
|
4 cups (c.) |
|
1 quart (qt.) |
|
2 pints (pt.) |
|
1 gallon (gal.) |
|
4 quarts (qt.) |
Examples,
8 fl. oz.
2 c X --------- = 16 fl. oz.
1 c
Here we used the fact that 1 cup = 8 fluid ounces.
1 gal
24 qt X --------- = 6 gal.
4 qt
Here we used the fact that 1 gallon = 4 quarts.
3.3 - Mass
Commonly referred to as "weight", although mass and weight have different meanings
in the scientific world.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Examples,
1 lb
24 oz. X --------- = 1.5 lb.
16 oz
Here we used the fact that 1 pound = 16 ounces. The answer could have also been written as 1 lb 8 oz
because 0.5 or half a pound = 8 ounces.
1 kg
22 lb X --------- = 10 kg.
2.2 lb
Here we used the fact that 1 kilogram = 2.2 pounds.
|
4.1 - Angles
A ray is one of the basic terms in geometry. We may think of a ray as a "straight" line that begins at a certain point and extends forever in one direction. The point where the ray begins is known as its endpoint. We write the name of a ray with endpoint A and passing through a point B as "ray AB" or as,
-->
AB
Note how the arrow heads denotes the direction the ray extends in: there is no arrow head over the endpoint.
--> -->
For example: Rays HG and AB
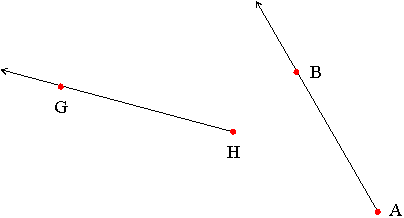
Two rays that share the same endpoint form an angle. The point where the rays intersect is called the vertex of the angle. The two rays are called the sides of the angle. Here are some examples of angles.
A
\ | / +-------
\ | / /
\ A |A / A /
+------- +------- +------- /
obtuse right acute reflex <----- angle
>90 90 <90 >180 <--- degrees
The reflex angle looks like any of the others, but it is measured around the back.
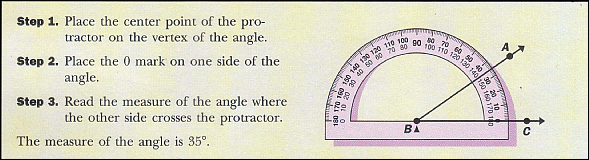
Here is how to use a protractor to measure an angle,
We can specify an angle by using a point on each ray and the vertex. The angle below may be specified as angle ABC or as angle CBA; you may also see this written as ⟨ABC or as ⟨CBA. Note how the vertex point is always given in the middle.
A
\
\
\
+--------- C
B
Two angles are called complementary angles if the sum of their degree measurements equals 90 degrees.
One of the complementary angles is said to be the complement of the other. For Example,
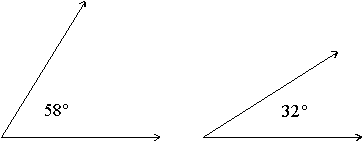
when glued together yield:
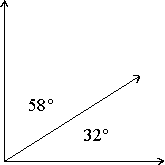
Two angles are called suplementary angles if the sum of their degree measurements equals 180 degrees. One of the supplementary angles is said to be the supplement of the other. For Example,

when glued together yield:
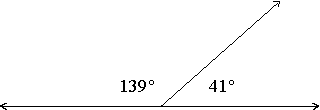
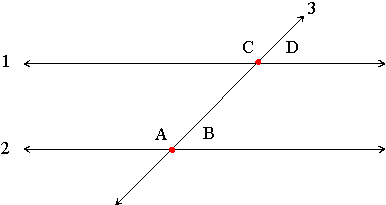
For any two lines that meet, such as in the diagram below, angle AEB and angle DEC are called vertical angles. Vertical angles have the same degree measurement. Angle BEC and angle AED are also vertical angles.
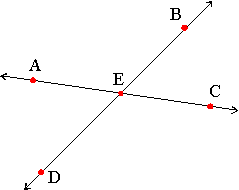
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle D are called alternate interior angles. Alternate interior angles have the same degree measurement. Angle B and angle C are also alternate interior angles.
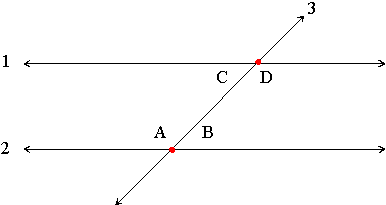
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle D are called alternate exterior angles. Alternate exterior angles have the same degree measurement. Angle B and angle C are also alternate exterior angles.
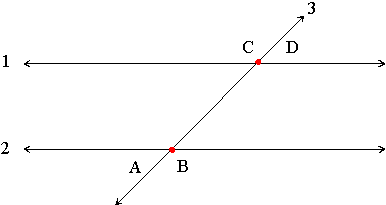
For any pair of parallel lines 1 and 2, that are both intersected by a third line, such as line 3 in the diagram below, angle A and angle C are called corresponding angles. Corresponding angles have the same degree measurement. Angle B and angle D are also corresponding angles.
An angle bisector is a ray that divides an angle into two equal angles. For example, the red ray on the right is the angle bisector of the angle on the left.
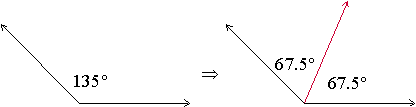
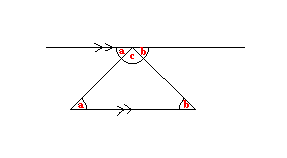
4.2 - Triangles
Triangles are three-sided shapes that lie in one plane. Triangles are a type of polygons. The angles in a triangle equal 1800.
Triangles can be classified according to the size of its angles. Some examples are right triangles, acute triangles and obtuse triangles.
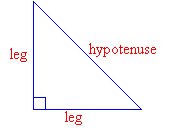
A right triangle is a triangle with a right (900) angle.
For example,
|
A right triangle has one other angle that is 350. What is the size of the third angle? |
You may have noticed that the side opposite the right angle is always the triangle's longest side. It is called the hypotenuse of the triangle. The other two sides are called the legs. The lengths of the sides of a right triangle are related by the Pythagorean Theorem.
An acute triangle is a triangle whose angles are all acute (less than 900). In the acute triangle shown below, a, b and c are all acute angles.
a
+
/ .
/ .
/ .
b +-------+ c
An obtuse triangle has one obtuse angle (greater than 900). The longest side called the hypotenuse is always opposite the obtuse angle.
For example,
|
Is it possible for a triangle to have more than one obtuse angle?
a b
+----+
/ .
/ .
/ .
/.
c +
|
Types of triangles can also be classified according to the length of its sides. For example equilateral, isosceles and scalene triangles.
An equilateral triangle has all three sides equal in length. Its three angles are also equal and they are each 600.
For example,
|
An equilateral triangle has one side that measures 5 in. What is the size of the angle opposite that side? 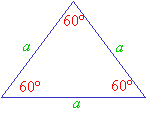
|
An isosceles triangle has two sides of equal length. The angles opposite the equal sides are also equal.
For example,
|
An isosceles triangle has one angle of 460. What are the sizes of the other two angles? 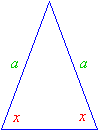
|
A scalene triangle has no sides of equal length. Its angles are also all different in size.
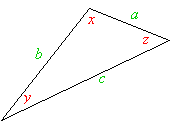
4.3 - Other polygons
A Polygon is a closed plane figure made up of several line segments that are joined together. The triangle is the simplest polygon. Each line segment is called a side of the polygon and a common endpoint of two line segments is called a vertex. The sides do not cross each other. Exactly two sides meet at every vertex.
For Example:
A B
+----------+
| |
| |
+----------+
D C
This rectangle is named ABCD
--> --> --> -->
Its line segments AB, BC, CD and DA
Its vertices are A, B, C, and D
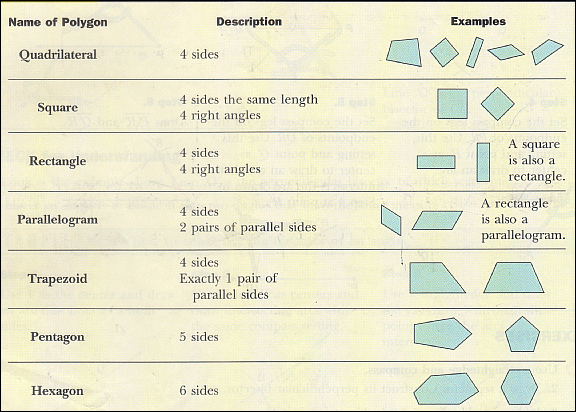
As shown in the following figure, polygons are classified according to the number of sides.
[1] A Beka Arithmetic 5, Work-Text, Pensacola, Florida
[2] J. Van de Walle. Elementary and middle school mathematics: Teaching developmentally, 5ed, Pearson, 2004
[3] D. Gale, Tracking the Automatic Ant, Springer, 1998
[4] H. P. Ginsburg, Children's Arithmetic, II edition, pro-ed, 1989
[5] D. R. Hofstadter, Metamagical Themas, Basic Books, Inc., 1985