It looks like the only reference to a mathematical operation is the word sum - so what operation will we have in this expression? If you said addition, you are correct.
The phrase 'a number' indicates that it is an unknown number - there was no specific value given to it. So we will replace the phrase 'a number' with the variable x. We want to let our variable represent any number that is unknown
Putting everything together, we can translate the given english phrase
with the following algebraic expression:
*'sum' = +
*'a number' = variable X
*'The sum of a number and 10' = X + 10
[1.1.b]
Again, we are wanting to rewrite this as an algebraic expression, not evaluate it.
This time, the phrase that correlates with our operation is 'product' - so what operation will we be doing this time? If you said multiplication, you are right on.
Again, we have the phrase 'a number', which again is going to be replaced with a variable, since we do not know what the number is.
Let’s see what we get for this answer:
*'product' = multiplication
*'a number' = variable X
The product of 5 and a number = 5X
[1.1.c]
First of all, we have the phrase 'less than' which mathematically translates as subtraction. You need to be careful with this phrase, it is very tempting to start off with 3 and put your subtraction sign after the 3. However, think about it, if you want 3 less than something, you are 3 below it. In order to be 3 below something, you would have to subtract the 3. So you would not have 3 minus, but minus 3 as PART of your expression.
The other part of the expression involves the phrase 'twice a number'.
'Twice' translates as two times a number and, as above, we will replace
the phrase 'a number' with our variable x.
Putting this together we get:
*'less than' = -
*'twice' = 2 times
*'a number' = variable X
*'3 less than twice a number' = 3 - 2X
[1.1.d]
First of all, the term 'quotient' is going to be replaced with what mathematical operation? If you said division, you are right on the mark.
Note how 3 immediately follows the phrase 'the quotient of', this means that 3 is going to be in the numerator. The phrase that immediately follows the word 'quotient' is going to be in the numerator of it.
After the word ‘and', you have the phrase 'the difference of a number
and 2'. That is the second part of your quotient which means it will
go in the denominator. And what operation will we have when we do
write that difference down below? I hope you said subtraction.
Let’s see what we get when we put all of this together:
*'quotient' = division
*'difference' = -
*'a number' = variable X
*'The quotient of 3 and the difference of a number and 2' = 3 / [X - 2]
1.2 - Slope, Intercepts, and Slope-Intercept Form
Straight-line equations, or linear equations, graph as straight lines, and have simple variables with no exponents on them.
For example, the linear function, f(x) = mx + b, may be graphed on the x, y plane as the equation,
In summary
Given some information about a line, you can figure out the equation of that line.
First you write the standard equation of a line,
Then plug in the numbers you are given. You've been given the slope m. The point (-1, -6), gives me an x-value and a y-value: x = –1 and y = –6. The slope-intercept form of a straight line has y, m, x, and b. So the only missing component is is b (the y-intercept).
y = mx + b
y = 4x + b <-- replace m with 4
y = 4(-1) + b <-- replace x with -1
-6 = 4(-1) + b <-- replace y with -6
-6 = -4 + b
-6-(-4) = b
-2 = b
The line equation is y = 4x – 2
1.3 - Graphing Linear Equations
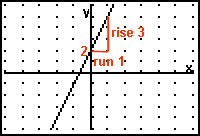
Follow the example y = 3x + 2 through this explanation.
This fraction is your rise/run.) slope = 3/1
(If rise is positive, move up. If rise is negative, move down.) (If run is positive, move right. If run is negative, move left.)
...
|
2.1 - Simultaneous Equations
When in a given problem, more than one algebraic equation is true at a time, it is said there is a system of simultaneous equations which are all true together at once. Such sets of multiple equations may help solve for more than one unknown variable in a problem, since having more than one unknown in one equation is typically not enough information to solve any of the unknowns.
...
|
3.1 - Monomials and Polynomials
An algebraic expression consisting of one term that is a constant, a variable, or the product of constants and variables is called a monomial. Examples of monomials are,
4 x 4y 7y2x3z
Two or more terms containing the same variables, with correspomnding variables having the same exponents
are called like terms. Examples of like terms are,
4x and x 5y and -7y
2x2 and 3x2 5z3 and 3z3
The degree of a monomial in one variable is the exponent of the variable. For example,
The degree of 4x is 1
The degree of 2x2 is 2
The degree of 5z3 is 3
The degree of a nonzero constant is zero. For example, 5 is the same as 5x0.
A monomial such as 7x3 may be considered a polynomial of one term. A polynomial is on its simplest form when it contains no like terms. For example,
5z3 + 2x2 + 3z3 + 4
The terms 5z3 and 3z3 are like terms and can be added up.
The simplified form of the polinomial is,
8z3 + 2x2 + 4
...
|
4.1 - Prime, Composite, and Square Numbers
...
|
5.1 - Quadratic Expressions, Equations, And Functions
...
[1] A Beka Algebra 1, Work-Text, Pensacola, Florida.